連休の後半、子どもさんたちと一緒に頭の体操してみましたか？
それでは【解答編】です。この【解答編】の画像は、この問題の元投稿であるTwitterの投稿主ロボ太さんの投稿から引用させていただき、一部解説用に加筆させていただきました。
ちなみに私はこちらの解法で答えを出しました。
①唯一長さが与えられている赤線（10cm）の部分が対角線となるように見立て、その4点を結ぶひし形（正方形）を考えます。そのとき、元の図形の一部で、新しく考えたひし形（正方形）からはみ出している部分を、足りない部分に移動させること（①→①’、②→②’、③→③’、④→④’））がポイントです。こうすることで、元の十字型の図形の面積と変形させて作り出したひし形（正方形）の面積が同じであることを確認します。（あえて、ひし形とし、正方形を（）書きで表記しているのは、面積計算の際に正方形の公式が適用できないからです。子どもたちに教える場合、ここを納得してもらうことが一番大切です。）
②ひし形の面積の公式に当てはめて計算します。
10×10÷2＝50
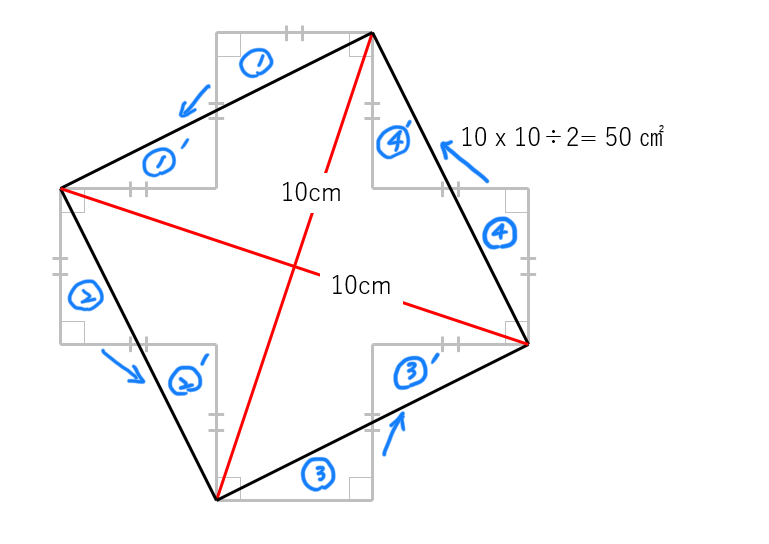
②ひし形の面積の公式に当てはめて計算します。
10×10÷2＝50
別解として次のような考え方も紹介されていました。
①元の図形を赤線の部分で2つに分け、場所を入れ替えること（元の図形のパーツを青斜線で示しておきました。）と、空いたスペースに同じパーツが2つ入ることで赤線の部分が1辺となる正方形と見立てます。本来のパーツだけでは新しい形を成立させることができず、追加のパーツを使うという考え方を子どもたちに理解してもらうところがポイントです。
②正方形の面積の公式に当てはめて計算し、元の図形は半分のパーツなので、忘れずに半分にします。
10×10÷2＝50
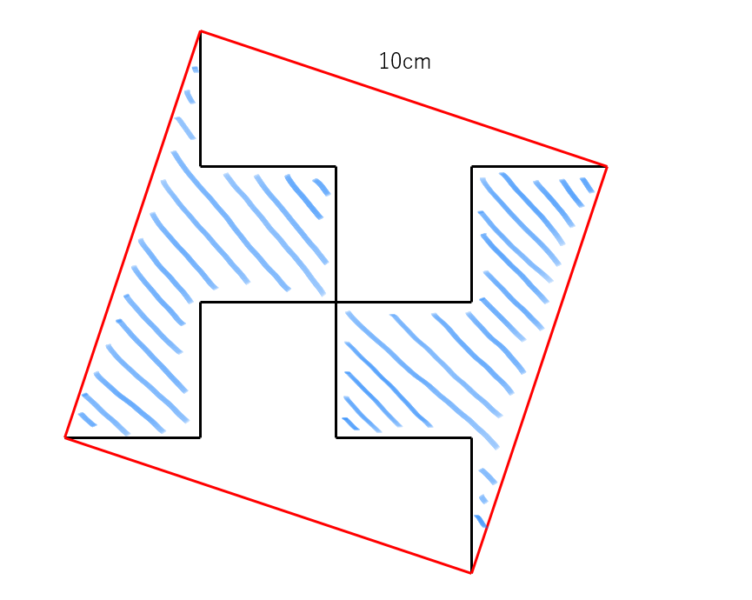
②正方形の面積の公式に当てはめて計算し、元の図形は半分のパーツなので、忘れずに半分にします。
10×10÷2＝50
この問題の場合、いずれの解法でも図形を変形させることが考え方の入り口になります。子どもたちと一緒に勉強する場合には、図に書いた状態だけで示してもなかなかイメージが付きにくいので、実際に紙で図形を作ってパーツを切り取り、パズルのように組み立てて、出来上がりをしっかりイメージできるようにすることが大切です。
こういった問題に強くなるには、何問も類題にチャレンジし、図形の変形の仕方のパターンを持っておくことです。その前にもっと大事な勉強の方法としては、しっかりパズル遊びをしておくこと。パーツの位置や向きを変えることで、目の前で見えている形がすべてではなく、図形に変化が起こるのだということを普段の遊びの中で感覚的に知っているかどうかが理解の深さに大きく影響してきます。
子どもたちが何気に遊んでいるように思えるパズル遊びは平面図形の学び、積み木遊びは立体図形の学びに欠かせないもの。小さい頃からそういった物で遊びこんでいるかどうかが学びの発展にはとても重要です。大人がそういう意図をもって遊び道具（教材）を選び、子どもたちと一緒にしっかり遊びこんであげましょう☆
