一昨日の本ブログ(『小学校で習う“四角形の概念”と“面積の公式”『だけ』で解いてみよう!!』)でご紹介しました小学生向けの算数の問題の【解答編】です。
(7+1)×(7+1)=64②正方形ABCDの4隅にある4つの三角形の合計を計算します。(三角形の面積の公式利用の場合)
7×1÷2=3.5
3.5×4=14※この部分の考え方は、4つの三角形を2つずつ引っ付けることで、2つの三角形ができることに気付ければ、四角形の面積の公式利用だけで、より簡単に計算することができます。(四角形の面積の公式利用の場合)
7×1=7
7×2=14③正方形ABCDの面積から4つの三角形の合計面積を引くことで、内側の正方形PQRSの面積を計算します。
64-14=50
ここからがポイント!!
ここまでは比較的簡単に求められると思います。この問題を小学生向けに解くためのポイントは、次に“四角形の概念”に気付けるかどうかというところ。
ここで今から考える内側の正方形PQRSを正方形のままとして面積を考えようと思ったら、一辺の長さを考えることになり、そうなると答えには平方根が必要になるし、そこから対角線を考えようと思ったら、三平方の定理や平方根の計算が必要になります。
正方形の特徴の一つは4辺の長さがすべて等しいということ。実は、4辺の長さがすべて等しいというのはひし形の特徴でもあります。(正方形とひし形の特徴の違いは、対角線の長さが等しいか等しくないかという違いだけ。)そうすると、ここまで正方形PQRSと考えていた図形をひし形PQRSと見ることができ、面積を求めるために使う公式が『対角線×対角線÷2』に変わります。
□×□÷2=50この式を解き進めると、□=10となり、対角線PRの長さは10cmになります。
細かいことを言えば、「④で作った式から□の値を出す計算で、“等式の性質”も必要じゃないのか?」とのご指摘を受けそうですが、そこは計算のルールで理解できるものとさせてください。実際の指導の際には“等式の性質”での説明が難しい場合は、図形によりひし形をもう一回り大きい正方形に変えるという考え方で“等式の性質”を使うことなく説明することはできます。今回はそこには触れませんが…。
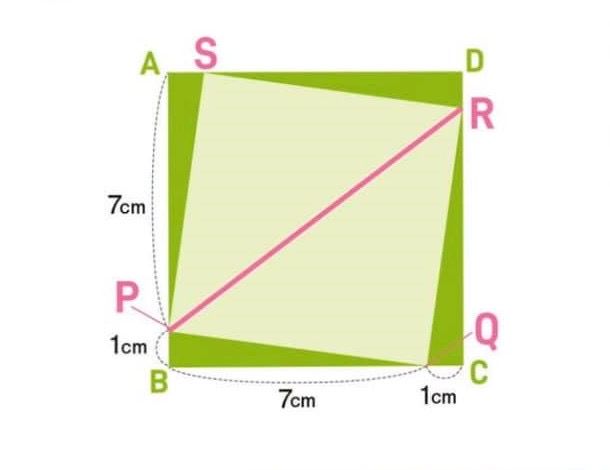
結論としては、先ほどポイントとして示した通り、正方形PQRSをひし形PQRSとして捉えられるかどうかというところ。この際に必要な“四角形の概念”さえクリアになれば、“面積の公式”だけで解くことができる問題となるので、小学生の算数の知識だけで解くことができる問題になります。
なまじ、数学の知識があると“三平方の定理”や“三角関数”などが先に頭に浮かんでしまうので、なかなかこの発想に辿り着けないので、逆にその知識がない小学生の方が、スムーズに算数の知識だけでこの問題を解くことができます。
もちろん、数学の知識を使っていけないわけではないので、それによって答えに辿り着ければ何も問題はないのですが、今回はあえて制約をかけることで、算数の問題とし、頭の体操としてご紹介させてもらいました。
どうでしたか?
小学生のお子さんをお持ちの保護者の方は、いつ子どもさんからこういった問題を「教えて!!」と言われないとも限らないので、たまにはこんな形で問題にチャレンジしてみておくのもいいかもしれませね☆
