先週、大学の授業で楓くんに出された宿題。
小学6年生の算数の面積を求める問題だが、これがなかなか一筋縄ではいかない難問ばかり。
楓くんも一週間かけて一生懸命考えたみたいでした。
円(扇形も含む)や四角形が複合型になっている図形の面積の問題。
代表的な問題の図はこんな感じです。
↓ ↓ ↓
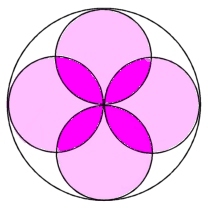
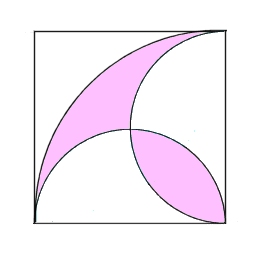
例えば、上の図の中の白い部分の面積を求めるとか、下の図のピンク色の部分を求めるって問題。
もちろん、一つの公式で簡単にできるようなものではなく、図形をバラバラにしたりしながら、いくつかの公式を組み合わせてやっと解ける問題です。
先週からずっと苦労していた楓くんに、前回会ったときに出したヒントは「その問題の図形を自分がさしやコンパスを使って描こうと思ったら、どうやったら描けるか考えてごらん。」というもの。
その図形を自分で描けるということは、その図形の仕組みがちゃんとわかっているということなので、それが問題を解く上ではとても大切なこと。
そのヒントで何問かは解けたみたいですが、それでもなかなか手強くて苦労してました。
結局、上の図の白の部分を求める問題あたりは最後まで解くことができず…。
今度は解き方のヒントを図示して渡しているので、それを見てもう一度チャレンジしてもらいたいと思っています。
こんな問題を解くときに大事なことは、「見るもの」と「見ないもの」を見つけ出すこと。
もっと具体的に言えば、問題で与えられている図の中ので、そこには書かれていないけど必要な線を見つけ出して見ることと、そこには見えている(書かれている)けど、その線を見ていたら惑わされるので見えているけど見ないようにする線を見つけて、自分の欲しい(求められる)形に図を変えて考えることが大切。
加えていうなら、一つの図をパズルのようにいくつかのパーツに分けて考えて、最後に加えたり引いたりしながら、最後に答えを組み立てることも大切。
もちろん、解き方も決して一つだけではないので、先述のヒントで全然わからないからといって諦めるんじゃなくて、自分なりに工夫してみると答えに辿り着けるはず。
勉強だからとか問題だからと固く考えるんじゃなくて、遊び心を持って、楽しみながらやると、こんな問題も「解いてみようかな?」って思えるようになるだろうし、数学(算数)嫌いの人も少しは好きになれるかも!?!?
がんばって想像力を働かせながら、頭の中のイメージを膨らませよう!!
