小学2年生のくり下がりのある筆算のひき算で、子どもたちがどのように理解し、どのような計算ルールで正解に辿り着いているか?
もちろん、学校の授業では、基本的な計算ルールを学びます。ただ、すべての子がその計算ルールのみで計算を行なうことはなく、必要に応じて、自分が理解しやすいルールや自分が間違えにくいルールを使って『正確に計算をする』というゴールに向かってがんばり、計算をします。
ただ、あたり前の話ですが、学校のテストでは、計算過程の理解を問われる問題では、学校の授業で教えた計算ルールのみが正解で、それ以外の計算ルールでの計算過程を答えていると不正解。特に、低学年なので穴埋め問題の形式なので、そこに入るべき答えは一つに限定されるような形ではありますが、文章の読み取り方(解釈に仕方)次第では、そこに別の答えが入ることもできなくはない。そして、その子にとっては、その計算ルールで計算方法をマスターし、正解を導き出しているので、自ずとその答えになるのもあたり前の話。
そして、その子にとっては「違うんだ…」というモヤモヤ感だけが残り、場合によってはがんばるモチベーションを失うことにもなりかねません。
具体的な問題で計算ルールの違いを示してみます。
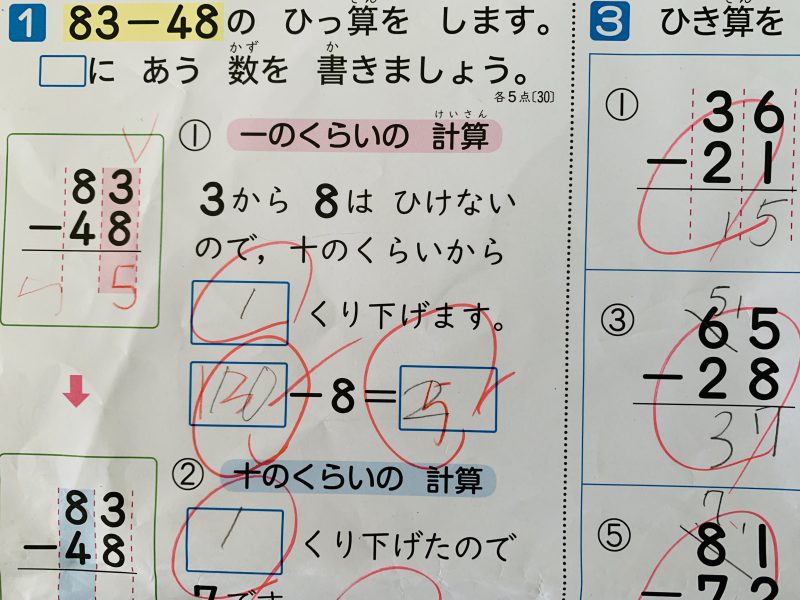
『83-48』を筆算でします。
一の位の計算で『3-8』がひけない場合、十の位から1(10)を借りてきて、『8』を『7』にします。
借りてきた1(10)と『3』で『13』とし、『13-8』をして、一の位に『5』の答えを立てます。
最後に十の位の『7-4』をして、十の位に『3』の答えを立て、計算の答え『35』が完成します。
一の位の計算で『3-8』がひけない場合、十の位から1(10)を借りてきて、『8』を『7』にします。(←ここまでは同じ)
借りてきた1(10)から先に『8』を引いて、その答えの『2』と元の一の位の『3』を足して一の位に『5』の答えを立てます。(←ここが学校の授業のルールと違います。)
最後に十の位の『7-4』をして、十の位に『3』の答えを立て、計算の答え『35』が完成します。(←ここも同じ)
この計算ルールに至る過程は、現在、小学校の算数でひき算の方法として指導されている“さくらんぼ”の考え方が関係してきます。
上の【学校の授業内容による計算ルール】の過程では、借りてきた1(10)と『3』で『13』とした後、『13-8』の計算をする際に“さくらんぼ”の考え方を適用すると、再び『10』と『3』とに分けて、『10』から『8』を引いた答えの『2』に残しておいた『3』を足して『5』を出します。
すなわち、一度合わせておいて、すぐに再び分解してしまうという、ある意味、無駄な手順が含まれる形になってしまいます。その過程を合理的に、くり下がりを行なった段階で“さくらんぼ”の考え方を適用して計算しているのが【子どもが理解している計算ルール】です。
手順が多くなることで、間違いにつながりやすくなる子たちにとって、その手順を一つでも簡略化することでミスを少しでも軽減し、間違わずに正解に辿り着く方法はとても重要です。
しかし、上記のように穴埋め問題の形式だと、【子どもが理解している計算ルール】による計算の方法を示す解答欄はなく、子どもはそのことには気付かずに自分が理解している計算ルールで穴埋めをしてしまうので不正解。いろんな意味で、ちょっと残念な気がしてます。
基本的な考え方がベースとなり、そこからいろんな形の派生があります。長年かかって出来上がった学習におけるスタンダードはそれが正解であることは間違いないですが、それが唯一の正解ではないこともまた事実。
我々が今生きているこの世の中は多様性の社会。それは学習場面においても同じことで、多様性は認められるべきこと。であるなら、計算ルールの多様性にも柔軟に対応でき、単にテストで正解・不正解という結果のみを求めるのではなく、総合的に判断し、評価してあげられるような仕組みも欲しいところ。
とは言え、それが一つの理想論であり、教育現場でその多様性すべてに対応することがどれだけ難しいかということもわかっています。
だから、せめて保護者のみなさんにはそのことをちゃんと理解しておいて、子どもたちが持ち帰ったテストを見て、単に正解・不正解だけで判断したり、点数だけで評価したりするのではなく、その子なりにがんばっている本質の部分をしっかり見て、理解して、評価してあげて欲しいと思います。
