“ロジカルシンキング(論理的思考)”。
学習場面に限らず、物事を考える上でもとても大切な思考。これができるかできないかは、その後の考え方や判断に大きな影響を与える。
だからこそ、学習の中でしっかり身に付けて欲しい力であることは間違いないのだが、現実的にはそこがほとんど育っていないのが現実であり、それは大人になっても同じ。まぁ、子ども時代にしっかり身に付けられていないので、大人になってもできていないのはあたり前の話なのですが…。苦笑
ロジカルシンキングの基本は、そのロジックの中で、与えられた要件を過不足なく、重複することなく使い切ると考えればわかりやすい(←説明の仕方がわかりにくい!?!?)と思いますが、じゃあ、実際、学校教育の授業の中ではどのあたりでこの内容を学んでいるか?
答えは、小学6年生の算数。
学習内容としては『場合の数』にあたる。わかりやすいところでは、サイコロの目の出方など、ある事柄の起こりうる場合の総数を考えるもの。もっと発展すれば、『和の法則』であったり、『積の法則』であったりを使いながら、場合の数を効率よく求めていくのであるが、基本的には、すべての事象を導き出し、その総数を数えることから始まる。
その中で、その手助けとなるものとして樹形図を使うことも多いだろう。
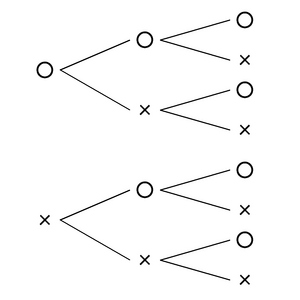
もちろん、この学習内容は、紹介したように小学6年生の算数における『場合の数』で止まる学習ではなく、中学校や高校での数学では『確率』であったり、『集合』などで、発展しながら学習する内容。これだけ段階分けをしながら学習するということは、それだけ大切な内容であるということ。のはずなのですが…。
「自分は苦手だなぁ…」と思う人は、小学6年生の算数テキストで、基本を学びましょう!!
身に付くと、社会生活等においても、とっても役に立つ力ですよ☆
