高校生1年生のIくん。今日の授業では数学Aの問題に悪戦苦闘。
と書き始めると、「やっぱり高校数学は難しいんだねぇ…。」と思われる方がほとんどだと思います。まぁ、たしかに決して簡単だとは言いませんが、必要以上に嫌ったり、苦手意識を持つ必要がないレベルまでいくのは、さほど難しくない教科だと思っています。
例えば、今日の授業の中でやっていたのは『チェバの定理』と『メネラウスの定理』。名前だけ聞いたり、定理の公式を見たりすると、これまた難しく感じるかもしれませんが、図形系の定理はいたってシンプルで、パターンがハッキリしているからそれさえ使いこなせたら、アプローチそのものは簡単な方の内容です。
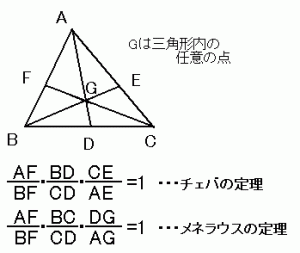
実際、どちらかと言えば、数学をそれほど得意としていないIくんもこれらの定理を使った問題もきちんとできていました。パターンにはめて立式するところまでは…。
どういうことかと言うと、式はできているのに、そこから式を解いて、答えに辿り着く過程の中で悩み、間違え、最終的に答えが出せずに苦労をしているのです。
そして、その悩んだり、間違えている内容はと言えば、高校数学の内容の『チェバの定理』や『メネラウスの定理』とは程遠い方程式の解き方のちょっとした応用だったり、比の考え方のこれまたちょっとした応用だったり…と言った中学校の数学や小学校の算数の授業内容のこと。もちろん、その基本的な問題はIくんもきちんと解けるのですが、この“ちょっとした応用”というのがミソなのです。
基本はできてるけど、ちょっと捻られると見事に引っかかってしまう。問題としては、どこで間違えたとしても不正解という結果。そうなると、本人的には、高校の数学が難しいから間違えるんだと思ってしまい、基礎の見直しを疎かにしてしまう。それでは間違いの修正には至らないのです。
発達障がいの子たちの特性にも合わせて…
「想像する」とか「決まってないことに対応する」といったことを苦手とするケースが多い発達障がいの子たち。そんな子たちにとって“ちょっとした応用”というのは、同じ問題の変化系ではなく、まったく新しいジャンルの問題と同じ。創意工夫する努力をしていないのではなく、その過程を生み出すこと自体が苦得手であり、それが特性の一つ。だから実際には習っていて、本当は本人ができる(解ける)力はあるのに、この“ちょっとした応用”という小さな壁が大きな壁となって邪魔をして、正解への道を閉ざし、嫌い(苦手)という気持ちをさらに大きくしてしまうのです。
じゃあ、どうすればいいのか?
簡単に言えば、応用を基本に変えてしまえばいい。方法としては2つのアプローチ。
1つは、考え得るできるだけ多くの応用を別のパターンとして暗記する方法に切り替える。
もう1つは、基本からちょっとした応用までを網羅できるように公式自体を工夫(覚えやすくして)覚えるようにする。
ただ、いずれも本人だけの力ではちょっと難しいので、サポートする人間と力を合わせてがんばる方法にはなりますが、できる喜びを感じたり、苦手意識をなくしたりするに繋がれるための最大限の努力をすることが大事です。
できることからコツコツと…。
考え得る工夫はすべてチャレンジしてみる。
成長への道は小さなことの積み重ねだけですよ☆
