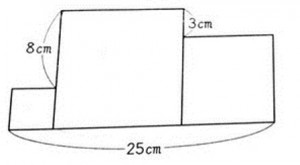
あるサイトにこんな投稿がありました。
上記の図の面積を求めよ!!という問題。小学生の4年生の息子さんの算数の宿題の問題を見て難しいと感じた保護者の方の投稿。もちろん、チャレンジしないわけがありません。
結果は…。
解けたけど、解けませんでした。
まるで禅問答のような結果報告。なぜこのような結果報告になるかというと、ちゃんと問題は解けて、正解は導き出せましたよ。一応、先生やってるので。でも、それは数学として解けたのであって、算数としての解き方は見つけられなかったということです。情けない…。(T_T)
これはずぅ~っと以前からわかっていて、自分の中でも苦手意識を持っていることなんですが、数学という算数より少し高度な力を学んだことですぐにそれに頼る頭になってしまって、算数というシンプルな考え方がどんどんできなく(閃かなく)なってしまったんです。
この問題も、数学の連立方程式を利用すれば簡単に解けます。この問題を解いてこのサイトに解答を投稿していた人の中には三元1次連立方程式を利用すれば簡単!!なんて人が多かったですが、実際には普通の連立方程式(二元1次連立方程式)で十分に解ける問題です。実際、自分もそれで解きました。
でも、それでは小学生の子には理解できないのでそんな方法での解説は通用しません。
投稿の中にはちゃんと算数として解いている人もいて、その解答を見ると「なるほど!!」と納得できるし、ものすごく簡単な解き方(考え方)で解答を導き出すことができるのです。
説明をする上でその方法を導き出さないといけない(解答がない)ときは、一旦数学として解いて正解を出した上で、答えから逆算して算数としての解き方を探すようにしてます。これまた情けない話ですが…。
進化(数学ができるようになる)することで退化(算数ができなくなる)しちゃってるという、何と言えばいいのかわからない話。だからと言って、「じゃあ、もう一度ちゃんと算数勉強すれば?」と言われても、頭がすでに数学頭になっちゃってるので、なかなかうまく切り替えることができないんですよねぇ……。^^;