中学3年生の数学の授業にて二次関数の問題に取り組む受験生。
二次関数の習い始めで「学校で授業聞いててもサッパリわからん…。」のコメントから始まったこの単元の学習。
・問題の基本式に与えられた数値を“代入”して表を完成し、グラフ上にその点を“座標”で示し、点を繋いでグラフを完成する。
・与えられグラフ上の2点の“座標”を求め、その2点間の“変化の割合”を求める。
・その2点を通る直線の式(“一次関数の式”)を“変化の割合”や“連立方程式”を利用しながら求める。
・その2点と原点を結んでできる“三角形の面積”を求める。
最終的にはこれぐらいの複合内容が一つの大問の中にいくつかの小問として盛り込まれたものが入試問題で出される感じであり、こんな感じの二次関数の問題はたいていの学校の入試問題で出題されています。
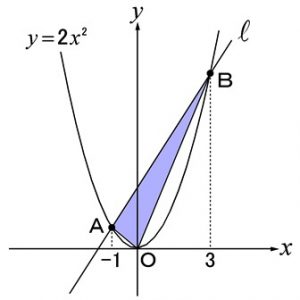
3年生のこの時期に習っている、一見複雑に見えるこのような問題で新しいことがいっぱいあるように見えますが、実際に習う新しいことは大きく言えば二次関数の基本形『y=ax2(axの2乗)』と『グラフは放物線になる』の2つぐらい。もちろん、細く言えばいくつかありますが、大まかに言っちゃえばここに集約されます。
実際、先の問題の中で“○○”で示してある文言は小学校の算数やこれまでの数学で習っている内容。そして、一つ一つの内容は、その時その時できちんとマスターしてから進んで来ているのに、こうやって別の問題に盛り込まれていると全然気付けなかったり解けなかったり…。
子どもたちの悩んでいるポイント
①表の数値をグラフ上に点としては取れるのに、グラフ上の点の座標を読み取るとなると悩む。
自分ができていることと悩んでいることは表裏の関係で、内容はまったく同じであり、単に聞き方(答え方)が違うだけなのに…。
②変化の割合はすでに一次関数で学習済み。でも、二次関数でまたその言葉に出会うとまったく別のものとして考えて悩む。たしかに一次関数では変化の割合=傾きで考えさせ、式を見ればすぐにわかるのであまり深く考えずに解いていたかもしれないけど、変化の割合の基本的な考え方は学習済みであり、解き方はまったく同じなのに…。
③2点を通る直線の式は完全に一次関数の内容であり、式の求め方でよく使用するのは連立方程式。普通に連立方程式の問題を与えたらスラスラ解くのに、二次関数の問題の中で連立方程式の考え方を求めるとなぜか違うやり方を始めて悩む。どちらも同じ連立方程式なのに…。
などなど……。
といった感じで、表裏の関係や学習済みの内容と今やっている内容との連動性に気付かず(気付けず)に「聞いていてもわからない」とか「習ったばかりだからわからない」という。それぞれの問題を解く力はちゃんとあるのだから、その力を別々の転として存在させず、きちんと結び合わせて線にすれば答えへの道筋は自分自身で立てられるのに、そもそもの入り口で難しく考えすぎている。本当にもったいないこと。
持っている知識を力をちゃんと出し切れるような、もうワンランク上の力をしっかり身に付けられるような本人の努力、そして身に付けさせてあげられるようなこちらの努力がまだまだ必要です。
